벡터

퍼온곳들

http://blog.naver.com/rbfwmqwntm?Redirect=Log&logNo=30110234072

http://goldface.tistory.com/6

http://hiddenviewer.tistory.com/32

http://navercast.naver.com/contents.nhn?rid=22&contents_id=4554

http://navercast.naver.com/contents.nhn?rid=22&contents_id=5121

http://kin.naver.com/qna/detail.nhn?d1id=11&dirId=1113&docId=55874522

http://gall.dcinside.com/board/view/?id=mathematics&no=48106

http://joy3x94.blog.me/70143319278

////////////////////////////////////////////////////////////////////////////////////////////////////////

 

 

 

벡터의 개념

 

보통 우리가 쓰는 수는 스칼라값으로 보면 된다. 하지만 이 값은 정적인 위치만을 기술하는 값으로

물체의 운동을 기술하기에는 부적하다.  이런 요구 충족을 위해 벡터량이 19세기 비교적 최근에 등장하게 되었다.

벡터는 크기와 방향을 갖는 물리량이다.

 

 

 

 

 

변위와 거리

 

변위는 움직인 거리로 마지막 위치에서 시작위치를 뺀 값이다.

하지만 거리는 중간에 거친 모든 경로를 더한 값이다. 변위는 중간에 일어나는 모든 일에 대한 정보는

사라진다는 점때문에 프로그램에서는 운동을 작은 시간간격으로 쪼개어 정보손실을 보완한다.

 

 

 

 

 

 

 

벡터의 크기_1

 

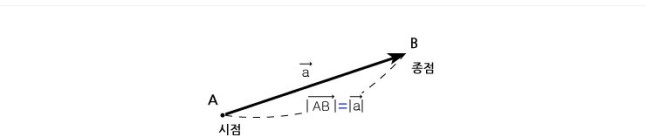
벡터는 위 그림과 같이 크기를 나타내는 선분 AB에 방향을 나타내는 화살표를 붙여 표현한다.

또, 선분 AB의 길이를 벡터  의 크기라 하고, 기호로 ||또는 |a|로 나타낸다. 벡터는 크기와 방향에

의해서만 정의되므로 다음 그림과 같이 크기와 방향이 같은 벡터는 모두 동일시 한다.

즉, 한 벡터를 평행이동하여 얻은 벡터는 모두 같은 것으로 여긴다는 것.

              

 

 

 

 

 

벡터의 크기_2

 

원점 O이고 종점이 A( a1, a2)인 벡터의 크기는 피타고라스의 정리를 이용하여 구할 수 있다.

즉, a=( a1, a2 )일때 아래와 같다.

              

                                                    

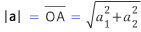
시점이 원점이 아닌 벡터의 크기도 이와 같이 피타고라스의 정리를 이용하여 구할 수 있다.

 

                                                        

                              

                        

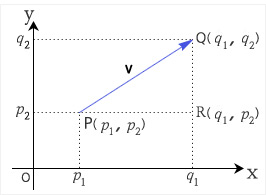
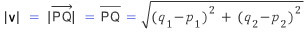
또한, 3차원의 공간 벡터로 확장시키면

 

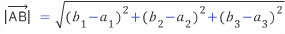
요렇게 된다.

 

 

 

 

 

역벡터와 영벡터

 

벡터 a와 크기는 같지만 방향이 반대인 벡터를 벡터 a의 역벡터라 하고 기호 -a로 나타낸다.

                                           

                                              

 

영벡터는 말그대로 방향도 크기도 없는 아무 힘없는 벡터.

따라서 벡터 + 역벡터 = 0 이 성립한다.

 

 

 

 

 

정규화 ( 노말라이즈 normailization )

 

벡터의 크기를 1로 맞추는 것을 의미한다. 벡터의 방향만을 사용하고 싶을 때,

크기가 1인 단위벡터로 만들어 사용하는 것이다.

예를 들어 두 오브젝트와의 거리를 정규화하여 두 사이를 0.6배로 줄인다는 계산을 한다던지 할 때 편리하다.

 

 

 

 

 

 

 

벡터의 합

 

 

 

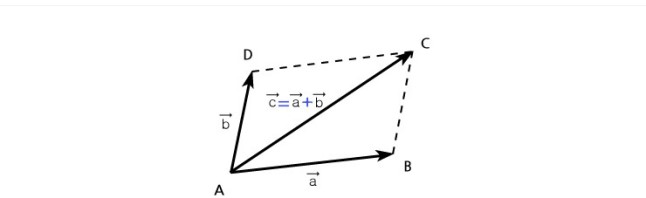
가래는 세 사람의 힘을 합쳐 큰 힘을 낼 수 있다.

 

 

 

 

 

 

위치벡터

 

위에서 얘기한데로 크기와 방향이 같은 벡터는 모두 같은 벡터이므로 시점을 일치시키면 벡터를 다루기 쉽다.

시점을 일치시킨다는 것은 원점 0이 있는 그래프인 좌표평면상으로 이동시켜본다는 것이다.

      위 그림에서 벡터 a에 대하여 a =  가 되는 점 A의 위치가 정해진다. 역으로 점 A에 대하여 벡터 a 역시 단 하나로 정해진다.

이와같이 일정한 원점 0를 시점으로 하는 벡터 를 원점 0에 대한 점 A의 위치벡터라 한다.

벡터 a와 점 A는 일대일로 대응한다.

 

 

 

 

벡터의 내적 ( dot product )

 

힘으로 생각하면, 내적은 두 힘이 서로간의 방향에 대해 영향을 주는 정도를 나타낸다고 보면된다.

만약 두 힘이 서로 직각을 이루고 있다고 생각하면 한 힘이 다른 힘의 방향에는 아무런 영향을 줄 수 없으므로

내적의 결과는 0이된다. 또 두 힘의 방향이 같다면 내적은 두 힘의 곱이 된다.

이를 계산해 보자

                                                     

|x|와 |y|

위 그림은 y벡터가 x축과 일치하는 것처럼 보이는데 이는 계산을 위해 기울인것뿐이고 실제로 벡터x, 와 벡터y는

어느 방향이든지 상관없다.

이때 점 x에서 y축으로 직각으로 선을 내려서 임의점 z를 찍어보자

원점 z까지의 길이를 임의로 |z|라 한다면 

cosΘ = |z|/|x|

|z| = |x| * cosΘ가 된다.

즉, 위 그림에서 벡터 x와 벡터 y가 90도까지 점점 더 벌어지면 임의의 점 z는 0에 수렴하게 되므로

90도 일때 내적은 0이 된다는 것을 알 수 있다.

 

이게 어디 쓰이냐,  그건 잘 모르겠고 우선 아래 쓸 외적의 방정식에 쓰인다.

 

 

 

 

벡터의 외적 ( cross product )

 

외적은 어떠한 각도 Θ를 이루는 두 벡터 x, y에 수직을 이루는 벡터를 찾아내는 것이다.

내적는 단순 크기의 곱이기때문에 결과가 스칼라이지만

외적는 결과가 벡터이다. 그래서 내적을 스칼라곱 외적을 벡터곱이라 부르기도 한다.

 

벡터 a와 벡터 b에 동시에 수직인 벡터는

벡터a * 벡터b로 구할 수 있다.

 

그리고 그 벡터의 크기는 벡터 a와 벡터 b 사이에 생기는 평행사변형의 넓이와 같다. 

                     

우선 위 그림과 같이 벡터 a,b로 평행사변형을 만들어 보자. 그러면 저 평행사변형의 높이는 |A|sinΘ가 된다.

 |B|   * |A|sinΘ 이니까

(가로) *   (세로)

결국 |AB| = |A||B|sinΘ이 된다.

 

http://blog.naver.com/PostView.nhn?blogId=gt7461&logNo=110121578817

의 글을 보면 자연의 원리와 규칙은 동일하게 적용되므로 의 크기가 당연히 평행사변형의 넓이여야 한다는데

사실 잘 모르겠다. 우선 통과.